【 – 高中作文】
第一篇 2017山东高考分段
《2017山东高考细目表》
第二篇 2017山东高考分段
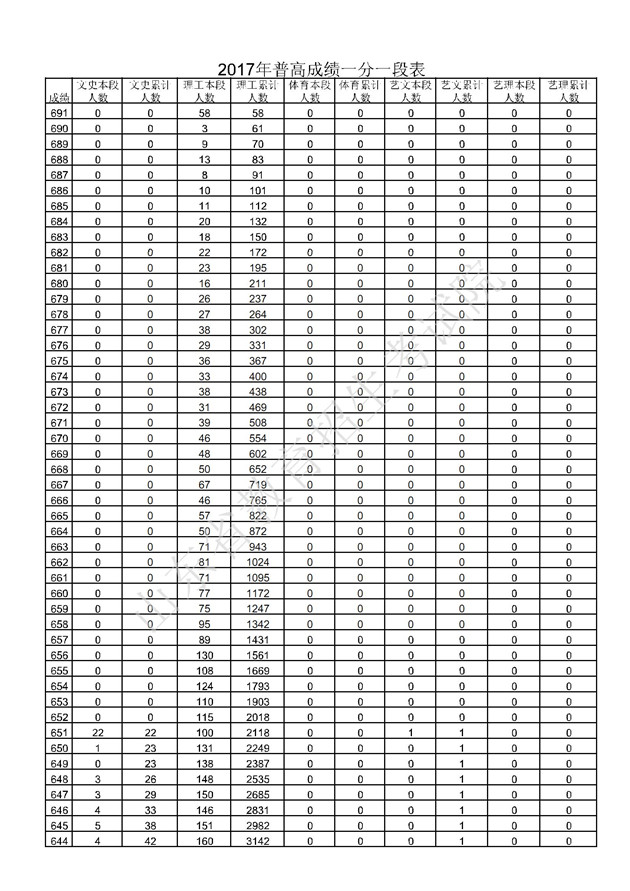
《2017年贵州高考成绩分段表》
2017年贵州高考分数线公布,同时还公布了2017年贵州高考成绩分段表,供考生志愿填报参考使用。2017年贵州高考本科一批文科分数线545分,理科456分。2017年贵州高考文科一本上线10703人。了解详情
高考落榜,人生不落榜。欢迎咨询贵阳北大青鸟学校。点击咨询
第三篇 2017山东高考分段
《【真题】2017年高考语文山东卷》
2017年高考山东卷
第I卷(共36分)
一、(每小题3分,共15分)
阅读下面一段文字,完成1~3题。
隆冬之际,西伯利亚的寒流(笼罩/席卷)欧亚大陆,狂风肆虐,草木凋凌,而那些春天的元素——温暖、雨水、绿叶、鲜花,都集结在位于热带的海南岛。海南岛就像是一艘花船,(系/停)在雷州半岛上,满载寒冬大陆的梦幻和想象。每年,从广州向漠河,春天昼夜兼程,都要进行一次生命版图的(扩展/扩充)。他像赤足奔跑的孩子,一路上用稚嫩的声音轻轻呼唤,于是万物苏醒,盛装应和,可谓“东风好作阳和使, 。”迢迢旅途中,气候的巨大差异,导致众多物种中只能有限地参与这一盛会。木棉花花朵硕大,是南国花中豪杰,“一声铜鼓催开,千树珊瑚齐列,”但她终究无法走出岭南。当春天行经长江、黄河流域时,出场的是桃花、杏花等新主角,“桃花嫣然出篱笑, ”,然而她们却无法追随春天深入雪国,陆续抱憾退出,随后登场的便是白杨、连翘等北国耐寒植物。
1. 文中加点的词语,有错别字的一项是
A. 肆虐 凋凌 B. 集结 昼夜兼程
C. 版图 稚嫩 D. 嫣然 抱憾退出
2. 依次选用文中括号里的词语,最恰当的一项是
A. 席卷 系 扩展 B. 笼罩 停 扩展
C. 席卷 停 扩充 D. 笼罩 系 扩充
3.在文中两处横线上依次填入诗句,衔接最恰当的一项是
A. 逢草逢花报发生 只恨春归我未归 B.万柄莲香一枕山 只恨春归我未归
C. 逢草逢花报发生 似开未开最有情 D.万柄莲香一枕山 似开未开最有情
4.下面语段中画线的成语,使用不恰当的一项是
2013年,郎平就任中国女排主教练。他知人善任,派不同队员参加不同比赛,充分发挥她们各自的优势。她眼光长远,在培养年轻球员,尤其是天才型球员时,
不揠苗助长。赛场上,她运筹帷幄,指挥若定,带领队员们屡创佳绩。2016年,中国女排勇夺里约奥运会冠军,不言而喻地证明了郎平执教水平的高超。
A.知人善任 B.揠苗助长 C.运筹帷幄 D.不言而喻
5.下面各句中,没有语病,句意明确的一项是2017山东高考分段
A.依托海量的普查成果,我国建成了包括重要地理国情要素、遥感影像及其他相关内容组成的地理国情数据库。
B.情景体验剧《又见敦煌》,昨天在新建的专属剧场首演,该剧以全新的观演模式带领观众进行了一次“古今穿越”。
C.这位前方记者采访到的专家表示,C919的试飞成功,标志着我国大型商用飞机的研制已达到国际先进水平。
D.骑自行车健身时,因为在周期性的有氧运动中使锻炼者能够消耗较多的热量,所以减肥、塑身效果都比较明显。
二、(每小题3分,共9分)
阅读下边的文字,完成6-8题
谈审美移情
所谓移情,通俗地说,就是指人面对天地万物时,把自己的情感移置到外在的天地万物身上去,似乎觉得它们也有同样的情感。当自己心花怒放时,似乎天地万物都在欢笑;苦闷悲哀时,似乎春花秋月也在悲愁。当然,天地万物不会欢笑,春花秋月也不会悲愁,是人把自己的悲欢移置到了他们身上。描绘此种移情现象的第一人是庄子。《庄子o秋水》篇中,庄子看见鱼儿“出游从容”,于是把自己在出游中体验到的快乐之情移置到鱼身上,觉得鱼在出游时也是快乐的。庄子所述,是典型的审美移情现象。
然而,对移情现象作出真正的理论概括是晚近的事。最早把移情作为一种美学观念提出来的是德国学者费舍尔父子。他们认为,我们对周围世界的审美观照,是情感的自发的外射作用,也就是说,审美观照不是主体面对客体时的感受活动,而是外射活动,即把自己的感情投射到我们的眼睛所感知到的人物和事物中去,在费舍尔父子那里,移情观念已大体上确定了,但通过形而上的论证把移情说提高到科学邢台的则是德国美学家立普斯。因为移情说的影响巨大,以至于有人把立普斯誉为美学界的达尔文。
审美移情作为一种审美体验,其本质是一种对象化的自我享受。这就是说,审美体验作为一种审美享受,所欣赏并为之感到愉快的不是客观的对象,而是自我的情感。在审美享受的瞬间,是人把自我的情感移入到一个与自我不同的对象(自然、社会、艺术中的事物)中去,并且在对象中玩味自我本身。
审美移情的基本特征是主客消融、物我两忘、物我同一、物我互赠。移情和感受不同。在感受活动中,主体面对客体,主客体是分离的,界限是清楚的。但在移情活动中,主体移入客体,客体也似乎移入主体,主客体融合为一,已不存在界限。对主体而言,他完全地沉没到对象中去,在对象中流连忘返,进入忘我境界;对客体而言,它与生命颤动的主体融合为一,实现了无情事物的有情化,无生命事物的生命化。也就是说,在移情之际,不但物我两忘、物我同一,而且物我互赠、物我回还。清代大画家石涛在描述自己创作的心理状态时所说的“山川脱胎于予,予脱胎于山川”“山川与予神遇而迹化”,就是审美移情中的物我互赠、物我回还的情境。
审美移情发生的原因是同情感与类似联想。谷鲁斯等人认为引起移情的原因是人的生理活动,移情源自于人的“内模仿”。但立普斯的观点更可信。他认为,审美移情起源于人的类似联想。人都有一种自然倾向或愿望,要把类似的东西放在同一个观点下去理解,所以总是按照切身经验的类比,去看待身外发生的事件。这就是说,审美的人都是有同情心,以自己体验到的某类情感,去类比、理解周围看起来是同类的事物。这种同情,不但及于他人,也及于其他生物及无生物。 审美移情的功能是人的情感的自由解放。尽管移情不一定伴随美感,但美感则必定伴随移情。因为审美移情能给人以充分的自由。人的不自由常常来自人自身。自身是有限的,它是自由的牢笼。可是在审美移情的瞬间,自身的牢笼被打破了,“自我”可以与天地万物相往来,获得了自由伸张的机会。“自我”与天地万物的界限消失了,人的情感也就从有限扩大到了无限。
(节选自童庆炳《中国古代心理诗学与美学》,有删改)

6.下列关于移情的表述,不正确的一项是
A.《庄子o秋水》中,庄子把自己出游中体验到的快乐之情移置到鱼身上,觉得鱼在出游时也是快乐的。这实际上是庄子对自己感情的对象化享受。
B.最早把移情作为一种美学观念提出来的,是德国学者费舍尔父子。但是,立普斯对移情的阐释才使得移情说具有了科学形态,他也因之深受赞誉。
C.在审美移情说看来,人的审美体验是主体在对客观对象的欣赏中,触生出千种情绪、万般感受,从而体验到审美对象所具有的独特的审美价值。
D.移情与感受不同。在感受活动中,主客二分,主体在客体面前保持自我,物我两立;而在移情时,主体与客体的界限被打破,主体客体相融合。
7、下列理解和分析,不符合原文意思的一项是
A.虽然对移情现象作出理论概括的主要是西方的美学家,不过《庄子o秋水》中对“鱼之乐”的记载表明我国的哲学家早已经描绘了这种现象。
B.关于审美移情的起因,曾经出现过不同的观点。谷鲁斯等人认为,引起移情的原因是人的生理活动,移情源自于人的“内模仿”,这种观点不可信。
C.审美的人以自己体验到的某类情感,去类比、理解周围看起来是同类的事物,这与人要把类似的东西放在同一个观点下去理解的自然倾向是一致的。
D.审美移情能让人的情感自由解放。美感必定伴随着移情,因为审美移情能帮人打破自身的有限性,让自我的必灵丰富化,给人带来充分的自由。
8、根据原文内容,下列理解和分析不正确的一项是
A.李白的“相看两不厌,只有敬亭山”、李商隐的“春蚕到死丝方尽,蜡炬成灰泪始干”等诗句,都体现了审美移情,是诗人把自己体验过的情感移置到景或物身上的结果。
B.郑板桥《竹石》诗:“咬定青山不放松,立根原在破岩中。千磨万击还坚劲,任尔东西南北风”从审美移情看,诗人审美欣赏的对象不是竹石,而是移入竹石形象中的自我情感。
C.北宋画家文与可画竹时,“其身与竹化,无穷出清新”。“身与竹化”所强调的是竹已化为画家的精神,获得了人的生命存在。这是移情中出现的物我两忘、物我同一的境界。
D.在“我见青山多妩媚,料青山、见我应如是”中,南宋词人辛弃疾以移情的方式把自己的深情移入青山,青山因此就妩媚起来。此时主题的情感是移置在青山中,只属于青山的。
第四篇 2017山东高考分段
《2017年高考分段测试1》
2017年高考分段测试(一)
(测试范围:集合与常用逻辑用语 函数、导数及其应用
)
时间:120分钟
一、选择题(共12小题,每小题5分,共60分)
1.[2015·江西九江一模]若集合A={x|1≤3x≤81},B={x|log2(x2-x)>1},则A∩B=( )
A.(2,4]
C.(-∞,0)∪(0,4] 答案 A
解析 因为A={x|1≤3x≤81}={x|30≤3x≤34}={x|0≤x≤4},B={x|log2(x2-x)>1}={x|x2-x>2}={x|x<-1或x>2},所以A∩B={x|0≤x≤4}∩{x|x<-1或x>2}={x|2<x≤4}=(2,4].
2.[2016·陕西质检]若f(x)是定义在R上的函数,则“f(0)=0”是“函数f(x)为奇函数”的( )
A.必要不充分条件 C.充分不必要条件 答案 A
解析 f(x)在R上为奇函数=>f(0)=0;f(0)=0=>/f(x)在R上为奇函数,如f(x)=x2,故选A.
3.[2016·山西质检]给定下列三个命题:
B.充要条件
D.既不充分也不必要条件 B.[2,4]
D.(-∞,-1)∪[0,4]
满分:150分
p1:函数y=ax+x(a>0,且a≠1)在R上为增函数; p2:a,b∈R,a2-ab+b2<0;
p3:cosα=cosβ成立的一个充分不必要条件是α=2kπ+β(k∈Z).则下列命题中的真命题为( )
A.p1∨p2 C.p1∨(綈p3) 答案 D
110
解析 对于p1,令f(x)=a+x(a>0,且a≠1),当a=f(0)= +0=1,f(-1)
22
x
B.p2∧p3 D.(綈p2)∧p3
12321-122
= -1=1,所以p1为假命题;对于p2,因为a-ab+b= a-b+≥0,所以p2为假
242命题;对于p3,因为cosα=cosβ<=>α=2kπ±β(k∈Z),所以p3是真命题,所以(綈p2)∧
p3为真命题,故选D.
4.[2015·山东威海一模]函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)上单调递增,则f(2-x)>0的解集为( )
A.{x|x>2或x<-2} C.{x|x<0或x>4} 答案 C
解析 由题意可知f(-x)=f(x),即(-x-2)(-ax+b)=(x-2)·(ax+b),(2a-b)·x=0恒成立,故2a-b=0,即b=2a,
则f(x)=a(x-2)(x+2).
又函数在(0,+∞)上单调递增,所以a>0.
B.{x|-2<x<2} D.{x|0<x<4}
f(2-x)>0,即ax(x-4)>0,解得x<0或x>4.故选C. 5.[2015·课标全国卷Ⅱ]设函数f(x)=ln(1+|x|)-立的x的取值范围是( )
1A. ,1 3
1
B. -∞,∪(1,+∞)
311
C. -, 33
11
D. -∞,-∪
33答案 A
解析 函数f(x)的定义域为R,又由题意可知f(-x)=f(x),故f(x)为偶函数. 当x>0时,f(x)=ln (1+x)-
11
y=ln (1+x)单调递增,y=-12
1+x21+x2
1
f(x)>f(2x-1)成1+x2
调递增,所以f(x)在(0,+∞)为增函数.
1
由f(x)>f(2x-1)<=>f(|x|)>f(|2x-1|),得|x|>|2x-1|,解得x∈ ,1.故选A.
3
x-sinx
的图象大致是(
) 6.[2015·济南模拟]函数f(x)=ln
x+sinx
答案 A
-x+sinx
解析 利用排除法求解.易知f(x)的定义域关于原点对称,因为f(-x)=ln
-x-sinxπx-sinx
=f(x),所以函数是偶函数,排除B和D;当x∈ 0,时,0<x-sinx<x+=ln
2x+sinxsinx,0<
x-sinxx-sinx
<0,排除C,故选A. ,ln
x+sinxx+sinx
1
7.[2016·唐山调研]已知函数f(x)=x3-2×2+3m,x∈[0,+∞),若f(x)+5≥0恒
3成立,则实数m的取值范围是( )
A.m≥
179
1B.m>92D.m<9
22017山东高考分段
2C.m≤9答案 A
解析 f′(x)=x-4x,x∈[0,+∞),令f′(x)=x(x-4)=0,则f(x)在(0,4)单调132
递减,在(4,+∞)上单调递增,所以f(x)的最小值为f(4)=×43-2×42+3m=-+3m,
33要使f(x)+5≥0恒成立,则f(4)+5=-
321717
3m+5=-3m≥0,解得m≥. 3392017山东高考分段
8.如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
1
①函数y=f(x)在区间 -3,-内单调递增;2017山东高考分段
21
②函数y=f(x)在区间 -3内单调递减;
2③函数y=f(x)在区间(4,5)内单调递增; ④当x=2时,函数y=f(x)有极小值; 1
⑤当x=-时,函数y=f(x)有极大值.
2则上述判断中正确的是( ) A.①② C.③④⑤ 答案 D
1
解析 当x∈(-3,-2)时,f′(x)<0,f(x)单调递减,①错;当x∈ -,2时,f′(x)>0,
2
B.②③ D.③
f(x)单调递增,当x∈(2,3)时,f′(x)<0,f(x)单调递减,②错;当x=2时,函数y=f(x)1
有极大值,④错;当x=-y=f(x)无极值,⑤错.故选D.
2
9.f(x)=2sinπx-x+1的零点个数为( ) A.4 C.6 答案 B
解析 ∵2sinπx-x+1=0, ∴2sinπx=x-1.
令h(x)=2sinπx,g(x)=x-1,f(x)=2sinπx-x+1的零点个数转化为求两个函数图象的交点个数.
2π

=2,分别画出两个函数的图象,如图所示, π
B.5 D.7
h(x)=2sinπx的周期T=
55
∵h(1)=g(1),h >g ,
22
g(4)=3>2,g(-2)=-3<-2,可知两个函数图象的交点一共5个, ∴f(x)=2sinπx-x+1的零点个数为5.
10.[2015·江西南昌一模]已知点P(x1,y1)是函数f(x)=2x图象上一点,点Q(x2,y2)是函数g(x)=2ln x图象上一点,若存在x1,x2使得|PQ|≤
1A.51C.2答案 A
2
解析 因为g′(x)=(2ln x)′=f(x)=2x的图象是斜率为2的直线,所以
2B.5D.1
25
成立,则x1的值为( ) 5
x
由2,解得x=1,从而曲线g(x)=2ln x在x=1处的切线方程为y=2(x-1),又直线y
2
x
=2(x-1)与直线f(x)=2x平行,且它们之间的距离为
225
=
522+ -1
2
因为|PQ|的最小值为
25
, 5